← Назад Далее →
2.1. Метод конечных разностей
Метод конечных разностей заключается в замене частных производных в дифференциальных операторах их приближенными значениями, выраженными через дискретные значения функции в узлах расчетной сетки. Например, производная по пространству может быть заменена на одно из следующих выражений:
$$\frac{\partial u}{\partial x} \approx \frac{u_{i+1}^{} -u_{i} }{h} ;{\rm\; \; \; }\frac{\partial u}{\partial x} \approx \frac{u_{i+1}^{} -u_{i-1} }{2h} .$$
Существует большое число других выражений, соответствующих производной по пространству. Аналогично, производной по времени соответствуют, например, следующие выражения:
$$\frac{\partial u}{\partial t} \approx \frac{u^{n+1} -u^{n} }{\rm\tau }; \frac{\partial u}{\partial t} \approx \frac{u^{n+1} -u^{n-1} }{2{\rm\tau }} (2.2)$$
Точность таких приближений зависит, в том числе, от точки, которой это значение приписывается.
Предположим, что функция \(u(x, t)\) является достаточно гладкой и разложим первую из этих разностей в ряд Тейлора в окрестности узла с номером \(i\).
$$\begin{array}{l} {\frac{u_{i+1}^{} -u_{i} }{h} =\left. \frac{1}{h} \left(\frac{\partial u}{\partial x} \cdot h+\frac{1}{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } h^{2} +\frac{1}{6} \cdot \frac{\partial ^{3} u}{\partial x^{3} } h^{3} +O\left(h^{4} \right)\right)\right|_{x_{i} } =} \\{=\left. \frac{\partial u}{\partial x} \right|_{x_{i} } +\frac{h}{2} \cdot \left. \frac{\partial ^{2} u}{\partial x^{2} } \right|_{x_{1} } +O\left(h^{2} \right)} \end{array}$$
Таким образом, первая разность приближает значение производной на левой границе расчетной ячейки с первым порядком по h.
Если провести такое разложение в точке \(x^{*} =0.5\left(x_{i} +x_{i+1} \right)\), то порядок аппроксимации повышается на единицу:
$$\frac{u_{i+1}^{} -u_{i} }{h} =\left. \frac{\partial u}{\partial x} \right|_{x^{*} } +\frac{h^{2} }{24} \cdot \left. \frac{\partial ^{3} u}{\partial x^{3} } \right|_{x_{1} } +O\left(h^{4} \right)$$
Наименьшая степень параметров расчетной сетки \(h,{\rm\tau }\), которая остается при разложении разностного выражения в ряд Тейлора, называется порядком аппроксимации.
Система алгебраических уравнений, получающаяся при замене производных в дифференциальном операторе конечными разностями, называется разностным оператором или разностной схемой.
Для одного и того же дифференциального оператора можно построить множество разностных схем. Например, для уравнения (2.1) с использованием разностных операторов (2.2) можно построить, в том числе, следующие разностные схемы:
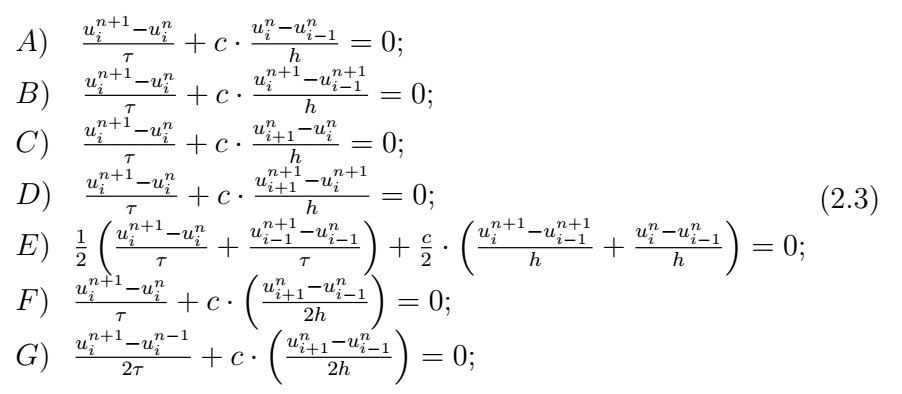
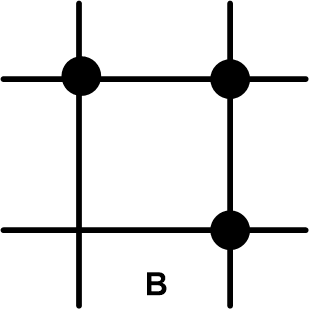
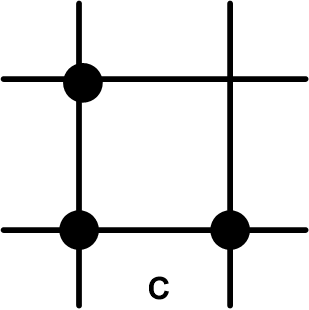
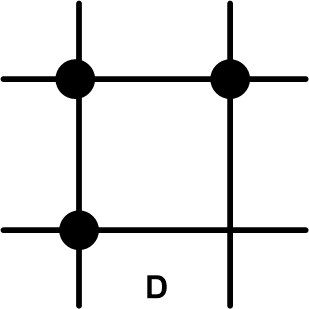
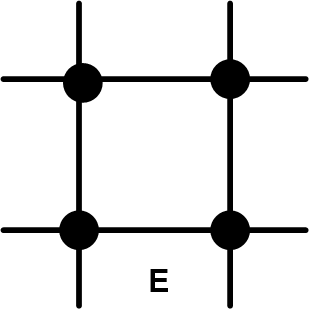
Множество узлов, используемых для построения разностного оператора, называют сеточным шаблоном разностной схемы. На рис. 2 представлены сеточные шаблоны схем из списка (2.3) в том порядке, в котором они там представлены.
По типу шаблона разностные схемы классифицируются по количеству используемых слоев по времени. В нашем примере это двухслойные (схемы A-F) и трехслойные (схема G). Другая классификация определяется количеством узлов шаблона на верхнем слое. Явные схемы (A, C, F, G) содержат на этом слое единственный узел, остальные схемы называются неявными (B, D, E). Начальные условия для трехслойных схем задаются на двух слоях. Для вычисления данных на втором слое можно использовать какую-либо двухслойную схему. В явных схемах искомая переменная на новом временном слое вычисляется по уже известным величинам на предыдущих слоях, в неявных схемах оказываются задействованными и другие переменные с нового слоя. При использовании неявных схем в общем случае приходится решать систему уравнений, однако для простейшего уравнения переноса неизвестные переменные находятся последовательно, начиная с левой границы (при c > 0), где задано граничное условие (метод «бегущего счета»).
 |
 |
 |
 |
 |
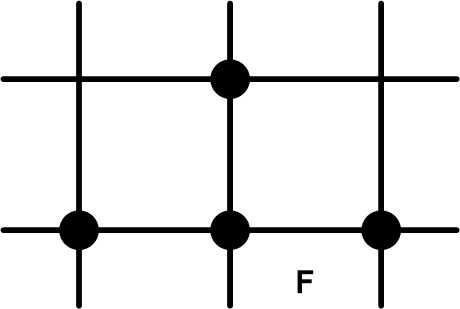 |
| Рис. 2. Вычислительные шаблоны разностных схем |
Разложим в ряд Тейлора оператор A из (2.3), который обычно называют разностной схемой «уголок», в узле с индексами \(\left(i,n\right)\):
$$\begin{array}{l} {u_{i}^{n+1} =u_{i}^{n} +\frac{\partial u}{\partial t} \cdot {\rm\tau }+\frac{1}{2!} \frac{\partial ^{2} u}{\partial t^{2} } \cdot {\rm\tau }^{2} +\frac{1}{3!} \frac{\partial ^{3} u}{\partial t^{3} } \cdot {\rm\tau }^{3} +...+\frac{1}{k!} \frac{\partial ^{k} u}{\partial t^{k} } \cdot {\rm\tau }^{k} +...} \\{u_{i-1}^{n} =u_{i}^{n} -\frac{\partial u}{\partial x} \cdot h+\frac{1}{2!} \frac{\partial ^{2} u}{\partial x^{2} } \cdot h^{2} -\frac{1}{3!} \frac{\partial ^{3} u}{\partial x^{3} } \cdot h^{3} +...+\frac{\left(-1\right)^{k} }{k!} \frac{\partial ^{k} u}{\partial h^{k} } \cdot h^{k} +...} \\{\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \frac{u_{i}^{n} -u_{i-1}^{n} }{h} =\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)+G\left(h,{\rm\tau }\right)} \end{array}$$
где
$$\begin{array}{l} {G\left(h,{\rm\tau }\right)=\left(\frac{1}{2!} \frac{\partial ^{2} u}{\partial t^{2} } \cdot {\rm\tau }-\frac{c}{2!} \frac{\partial ^{2} u}{\partial x^{2} } \cdot h\right)+\left(\frac{1}{3!} \frac{\partial ^{3} u}{\partial t^{3} } \cdot {\rm\tau }^{2} +\frac{c}{3!} \frac{\partial ^{3} u}{\partial x^{3} } \cdot h^{2} \right)+} \\{+\left(\frac{1}{k!} \frac{\partial ^{k} u}{\partial t^{k} } \cdot {\rm\tau }^{k-1} -\frac{c\left(-1\right)^{k} }{k!} \frac{\partial ^{k} u}{\partial h^{k} } \cdot h^{k-1} \right)+...} \end{array} (2.4)$$
Правая часть разложения разностного оператора в ряд Тейлора, содержащая производные всех порядков, называется его дифференциальным приближением.
Производные по времени, входящие в дифференциальное приближение, на решениях дифференциального оператора (2.1) можно выразить через пространственные производные:
$$\frac{\partial ^{k} u}{\partial t^{k} } =\left(-c\right)^{k} \cdot \frac{\partial ^{k} u}{\partial x^{k} } (2.5)$$
Произведя такую замену в (2.4) придем к выражению
$$\begin{array}{l} {G\left(h,{\rm\tau }\right)=P\left(h,{\rm\tau }\right)=\frac{c}{2!} \cdot \frac{\partial ^{2} u}{\partial x^{2} } \left(c\cdot {\rm\tau }-\cdot h\right)+\left(-1\right)^{3} \frac{c}{3!} \cdot \frac{\partial ^{3} u}{\partial x^{3} } \left(c^{2} {\rm\tau }^{2} -h^{2} \right)+} \\{+\left(-1\right)^{k} \frac{c}{k!} \cdot \frac{\partial ^{k} u}{\partial x^{k} } \left(c^{k-1} \cdot {\rm\tau }^{k-1} -\cdot h^{k-1} \right)+...} \end{array} (2.6)$$
которое называется P - формой дифференциального приближения. В свою очередь выражение (2.4) называют еще G - формой дифференциального приближения. Члены разложения (2.6) с самыми низкими степенями параметров \(h,{\rm\tau }\) называют первым дифференциальным приближением.Таким образом, первое дифференциальное приближение схемы «уголок» (simplest upwind) имеет вид:
$$\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \frac{u_{i}^{n} -u_{i-1}^{n} }{h} =\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)+\frac{c}{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } \left(c\cdot {\rm\tau }-\cdot h\right); (2.7)$$
Выпишем первые дифференциальные приближения других схем из списка (2.3). Для схемы B - «неявный уголок»:
$$\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \frac{u_{i}^{n+1} -u_{i-1}^{n+1} }{h} =\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)-\frac{c}{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } h; (2.8)$$
Если разложение этой схемы в ряд провести относительно другого узла, а именно, узла с индексами \(\left(i,n+1\right)\)то результат изменится:
$$\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \frac{u_{i}^{n+1} -u_{i-1}^{n+1} }{h} =\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)-\frac{c}{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } \left(h+c{\rm\tau }\right); (2.9)$$
Вид первого дифференциального приближения зависит, таким образом, от точки, в которой производится разложение. Для всех следующих схем в качестве такой точки выберем узел \(\left(i,n\right)\). Для схем (C, D) получаем:
$$\begin{array}{l} {C){\rm\; \; \; }\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \frac{u_{i+1}^{n} -u_{i}^{n} }{h} =\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)+\frac{c}{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } \left(h+c{\rm\tau }\right);} \\{D){\rm\; \; }\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \frac{u_{i+1}^{n+1} -u_{i}^{n+1} }{h} =\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)+\frac{c}{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } \left(h-c{\rm\tau }\right);} \end{array} (2.10)$$
для симметричной неявной схемы E - схемы Карлсона:
$$\begin{array}{l} {\frac{1}{2} \left(\frac{u_{2} -u_{1} }{{\rm\tau }} +\frac{u_{3} -u_{4} }{{\rm\tau }} \right)+c\frac{1}{2} \left(\frac{u_{1} -u_{4} }{h} +\frac{u_{2} -u_{3} }{h} \right)=} \\{=\left(\frac{\partial u}{\partial t} +c\frac{\partial u}{\partial x} \right)+\frac{c}{12} \frac{\partial ^{3} u}{\partial x^{3} } \left(h^{2} -2c^{2} {\rm\tau }^{2} -ch{\rm\tau }\right);} \end{array} (2.11)$$
для схемы Fс симметричной аппроксимацией пространственной производной:
$$\begin{array}{l} {\frac{u_{i}^{n+1} -u_{i}^{n} }{{\rm\tau }} +c\cdot \left(\frac{u_{i+1}^{n} -u_{i-1}^{n} }{2h} \right)=} \\{=\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)+\frac{c^{2} }{2} \cdot \frac{\partial ^{2} u}{\partial x^{2} } \cdot {\rm\tau }+\frac{c}{6} \cdot \frac{\partial ^{3} u}{\partial x^{3} } \cdot h^{2} } \end{array} (2.12)$$
для трехслойной схемы G, которую называют схемой «крест» (leap frog):
$$\frac{u_{i}^{n+1} -u_{i}^{n-1} }{2{\rm\tau }} +c\cdot \left(\frac{u_{i+1}^{n} -u_{i-1}^{n} }{2h} \right)=\left(\frac{\partial u}{\partial t} +c\cdot \frac{\partial u}{\partial x} \right)+\frac{c}{6} \cdot \frac{\partial ^{3} u}{\partial x^{3} } \left(h^{2} -c^{2} {\rm\tau }^{2} \right); (2.13)$$
Первое дифференциальное приближение, помимо исходного дифференциального оператора, содержит дополнительные (возмущающие) члены - более высокие производные, пропорциональные степеням \(h^{{\rm\alpha }} ,{\rm\tau }^{{\rm\beta }}\). Величины этих степеней \({\rm\alpha }\) и \({\rm\beta }\) называются порядком аппроксимации разностной схемой исходного дифференциального оператора. Так схема «уголок» аппроксимирует уравнение переноса с первым порядком как по пространству, так и по времени. Схема «крест» имеет второй порядок аппроксимации по \(h\) и \({\rm\tau }\), схема F - первый порядок по времени, и второй по пространству.
← Назад Далее →