Характеристическое уравнение для этой схемы имеет вид:
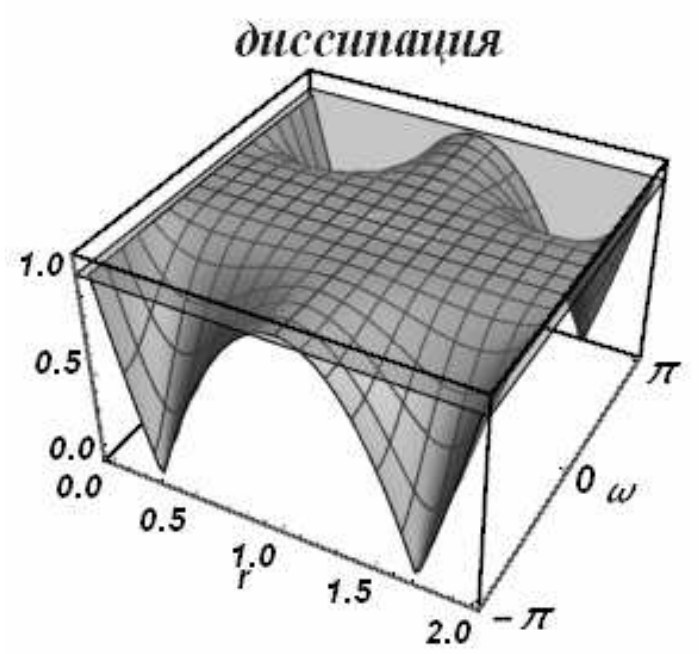
Область устойчивости этой схемы шире, чем у рассмотренных ранее схем и покрывает отрезок \(r\in \left[0,2\right]\). Ее диссипативная и дисперсионная поверхности представлены на рис. 12.
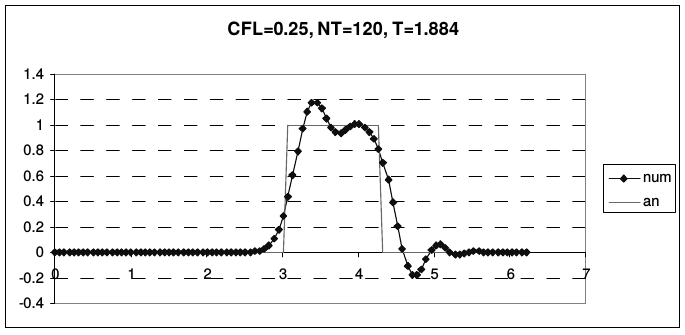
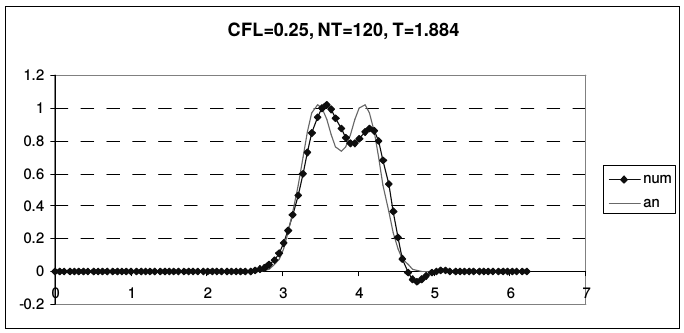
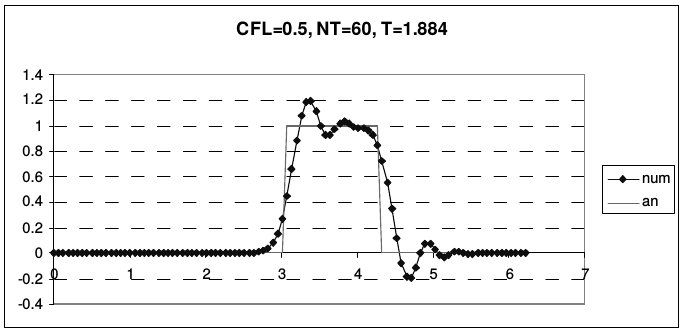
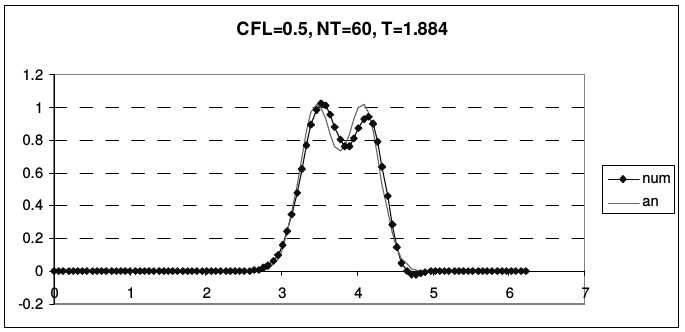
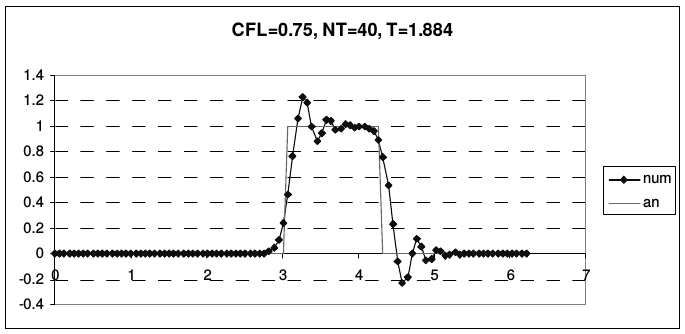
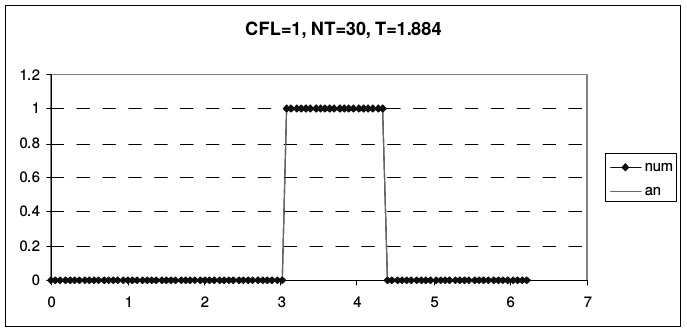
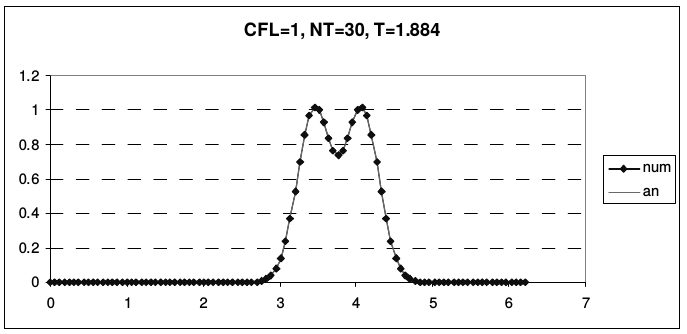
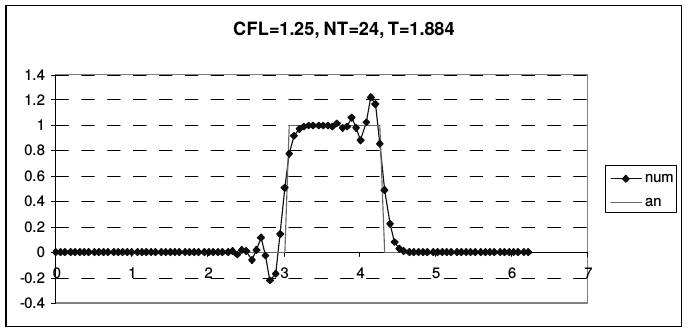
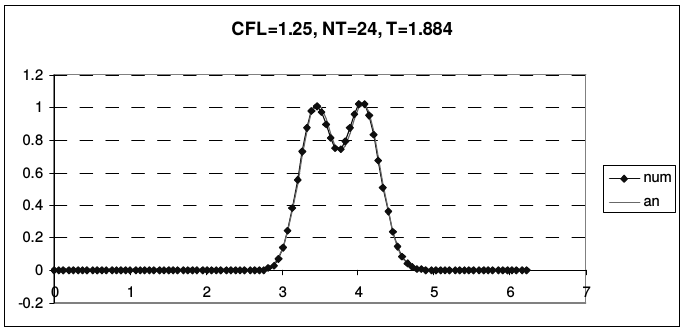
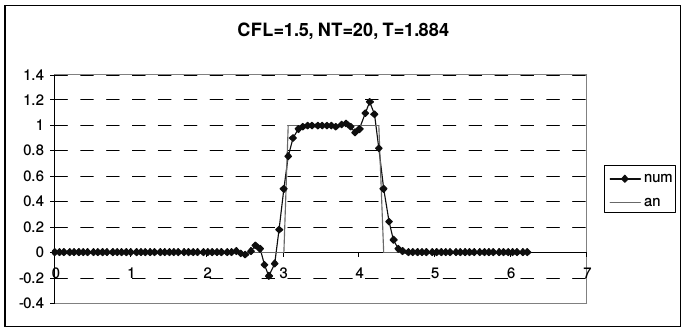
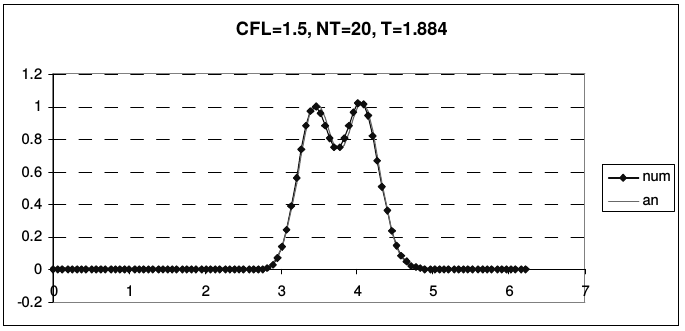
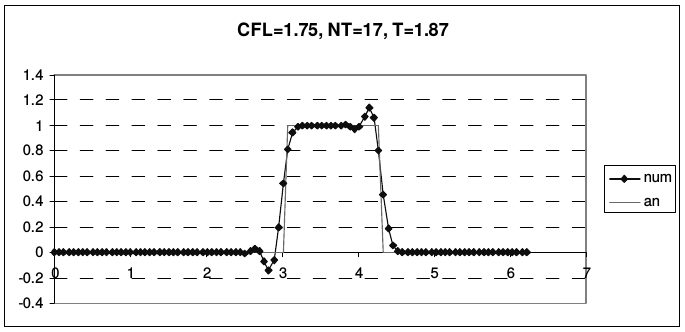
Дисперсия схемы Бима-Уорминга является аномальной при \(r < 1\) и нормальной, при \(1 < r < 2\). Из приведенных рисунков видно, что при \(r = 1\) и \(r = 2\) гармоники при всех приведенных волновых числах не затухают и не диспергируют. У схемы, таким образом, имеется два канала высокой точности, причем один из них находится на границе области устойчивости, а второй - в ее середине. При числах Куранта, близких к единице, схема проявляет аномально высокое качество сеточного переноса. На рис. 13 и 14 представлены результаты переноса тестовых профилей (2.43) по схеме Бима-Уорминга при разных числах Куранта.
 |
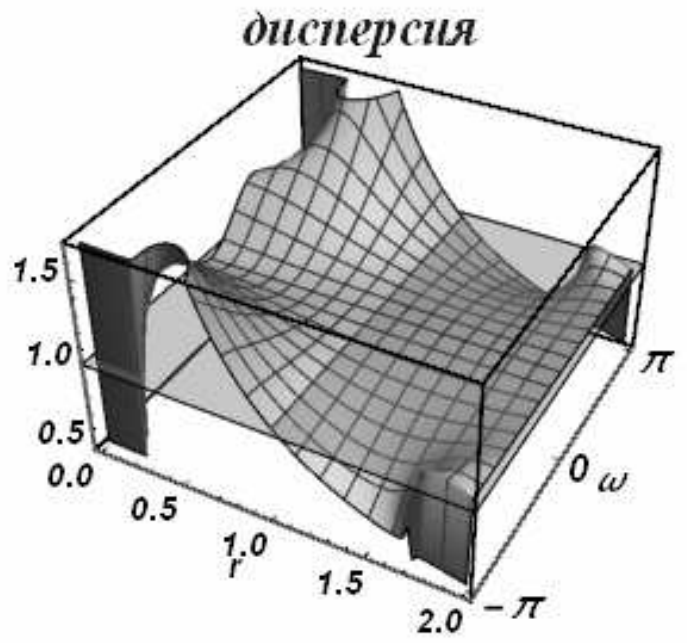 |
| а) | б) |
| Рис. 12 | |
 |
 |
 |
 |
 |
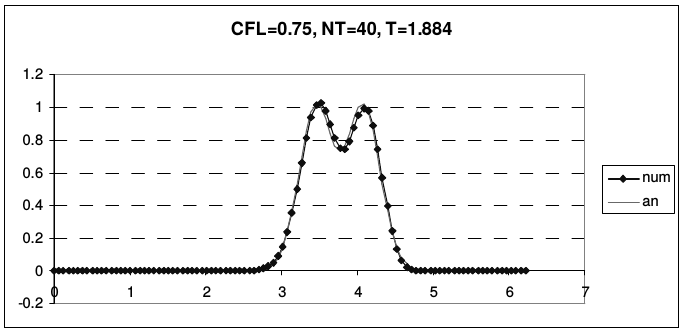 |
| Рис. 13. Схема Бима-Уорминга при числах Куранта, меньших единицы | |
 |
 |
 |
 |
 |
 |
 |
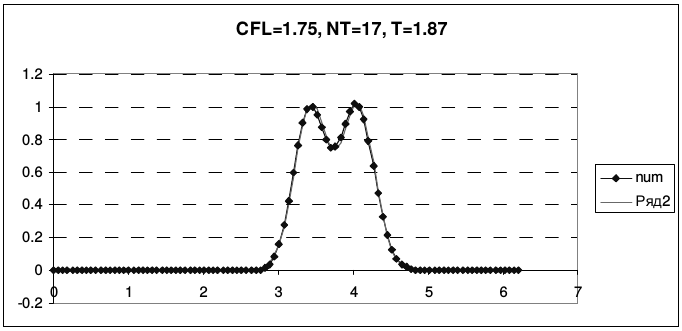 |
| Рис. 14. Схема Бима-Уорминга при числах Куранта от 1 до 2 | |