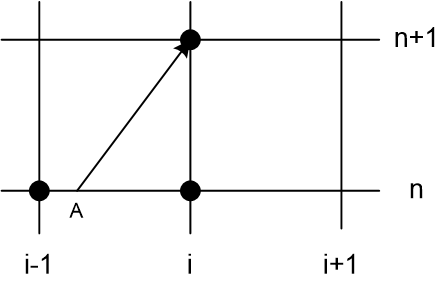
Более наглядный и менее затратный способ построения дискретных операторов для гиперболических уравнений связан с геометрической интерпретацией их решений. Известно, что решение дифференциального оператора переноса (2.1) остается постоянным на характеристиках - прямых линиях на плоскости \(\left(x,t\right)\), с коэффициентом наклона \(k={\Delta t\mathord{\left/ {\vphantom {\Delta t \Delta x}} \right. } \Delta x} ={1\mathord{\left/ {\vphantom {1 c}} \right. } c}\). Через узел \(\left(i,n+1\right)\) проведем прямую с наклоном \(k\) (характеристику) и найдем точку ее пересечения с временным слоем \(t_n\) (точка А, рис. 3а). Определим безразмерный параметр \(r={c{\rm\tau }\mathord{\left/ {\vphantom {c{\rm\tau } h}} \right. } h}\) - т.н. число Куранта-Фридрихса-Леви. Нетрудно видеть, что при \(0\le r\le 1\) точка А будет находиться между узлами с номерами \(\left(i\right)\) и \(\left(i-1\right)\) на расстоянии \(rh\) от правого узла и \(\left(1-r\right)h\)- от левого.
Поскольку решение на характеристике постоянно, то \(u_{i}^{n+1} =u\left(x_{A} ,t_{n} \right)\) и остается только применить интерполяционную формулу, вычисляющую с заданной точностью значение функции в точке А по известным ее значениям в узлах на текущем слое \(t_n\). Такой подход получил название метода обратной характеристики.
Рассмотрим простейшую линейную интерполяцию по двум ближайшим точкам. В этом случае
Таким образом, мы пришли к схеме «уголок». Линейная интерполяция привела к схеме первого порядка аппроксимации.
 |
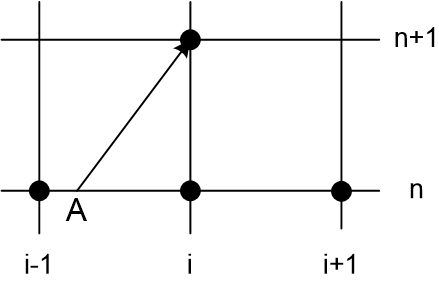 |
| а) | б) |
| Рис. 3 | |
Для квадратичной интерполяции необходимы три точки. Выберем в качестве таковых узлы с номерами \(i-1,{\rm\; \; }i,{\rm\; \; }i+1\)(рис. 3b) и построим интерполяционный квадратичный полином Лагранжа:
где
Интерполяционная формула (2.27) эквивалентна разностной схеме Лакса - Вендроффа:
Эту схему часто записывают в т.н. двухэтапной форме. На первом этапе по схеме Лакса вычисляются промежуточные значения \(u_{i+1/2}^{n+1/2}\)в центрах ячеек:
На втором этапе по схеме «крест» находятся неизвестные значения функции на новом временном слое:
Схема Лакса-Вендроффа имеет второй порядок аппроксимации на решениикак по времени, так и по пространству. Анализ других ее свойств будет проведен позднее.
Следует отметить, что все последующие схемы, получаемые квадратичной интерполяцией, будут иметь второй порядок аппроксимации на решении исходного дифференциального уравнения. Это следует из того, что начальные данные, заданные в виде параболы, будут переноситься по характеристикам на новый временной слой точно, без каких либо искажений.
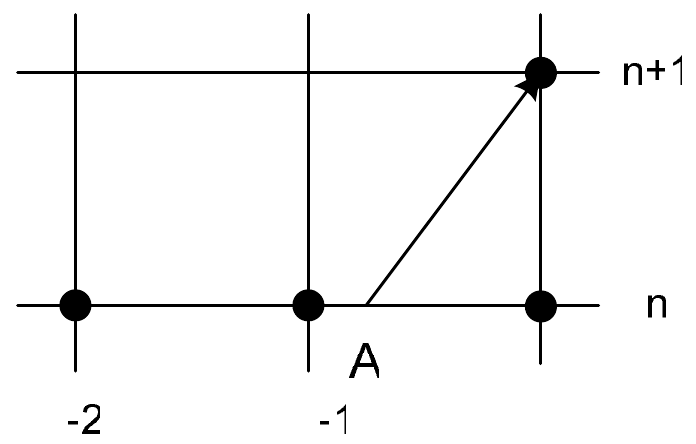
Если использовать для построения квадратичного полинома узлы \(i-2,{\rm\; \; }i-1,{\rm\; \; }i\), (рис. 4а) то квадратичная интерполяция дает:
где
Подставляя сюда координаты узлов \(x_i = ih\)получаем:
и приходим к разностной схеме Бима-Уорминга
 |
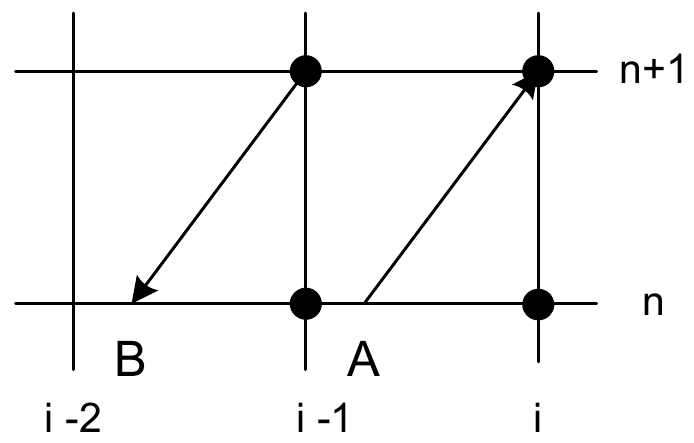 |
| а) | б) |
| Рис. 4 | |
При увеличении количества используемых узлов на текущем временном слое и повышения порядка полиномов Лагранжа, порядок аппроксимации также будет повышаться.
Для включения в описанную схему действий узлов сетки, расположенных на других временных слоях, значения, заданные в этих узлах, сносятся на текущий слой по характеристикам. Проиллюстрируем это на примере шаблона E для схемы Карлсона (рис. 4в). Построим точку B пересечения характеристики из узла \(\left(i-1,n+1\right)\) с текущим временным слоем: \(x_{B} =\left(i-1\right)h-rh\) и снесем в нее значение сеточной функции из узла \(\left(i-1.n+1\right):u\left(B\right)=u_{i-1}^{n+1}\). Интерполяционная формула в этом случае выглядит как:
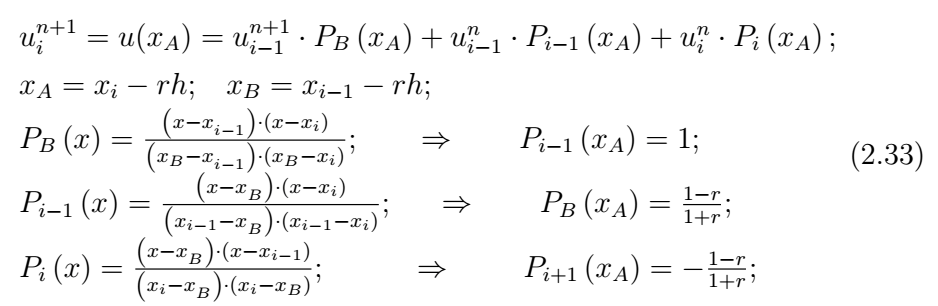
Для трехслойной явной схемы «крест» (рис. 5а) на текущий временной слой сносится значение сеточной функции со слоя \(n - 1\). Проведем характеристику из узла с номером \(\left(i,n-1\right)\), расположенном на слое \(\left(n-1\right)\), до пересечения с текущим слоем в точке B с координатой \(x_{B} =x_{i} +hr\). В эту точку переносится значение сеточной функции из узла \(\left(i,n-1\right)\): \(u\left(B\right)=u_{i}^{n-1}\). Интерполяционный полином строится по токам \(x_{i-1} ,{\rm\; }x_{i} +rh,{\rm\; }x_{i+1}\):
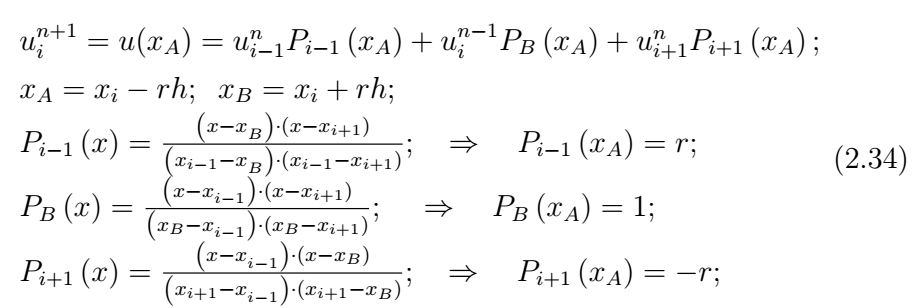
В результате приходим к выражению:
 |
 |
| а) | б) |
| Рис. 5 | |
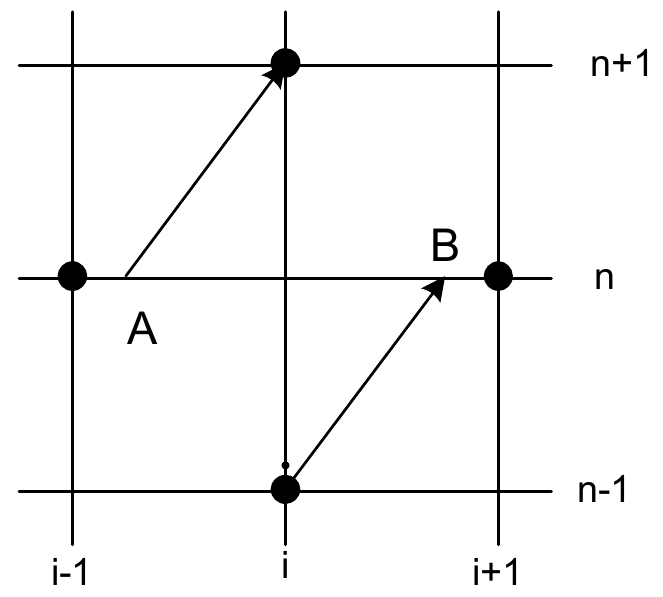
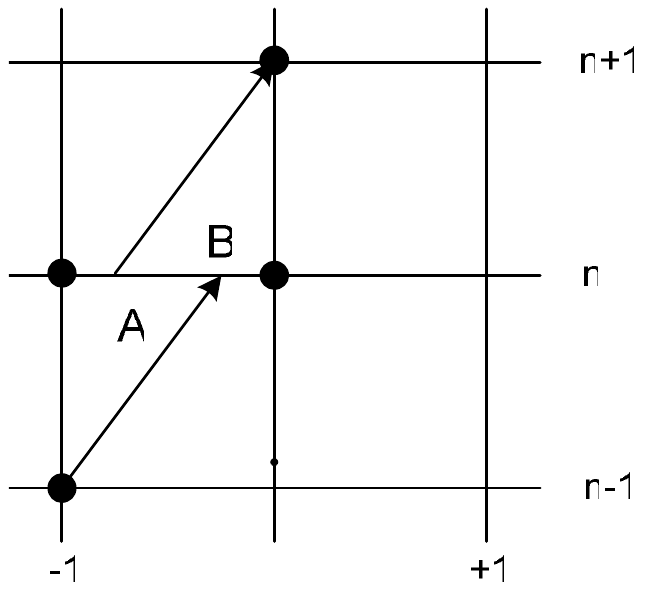
В заключение этого раздела рассмотрим трехслойный вычислительный шаблон (рис. 5в), состоящий из узлов с номерами \(\left(i,n\right);\left(i-1,n\right);\left(i-1,n-1\right);\left(i,n+1\right)\). Интерполяционный многочлен строится по трем узлам \(\left(i,n\right);\left(i-1,n\right);\left(i-1,n-1\right)\)и имеет вид:
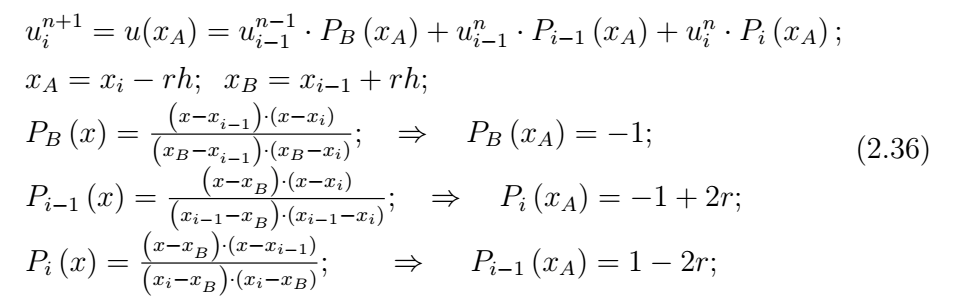
В результате приходим к разностной схеме, известной под названиями «КАБАРЕ» и схема Айзерлиса