Выражение для разностной схемы, полученное описанной выше функцией BuildScheme, аппроксимирует на решении уравнение переноса со вторым порядком, но, для многих шаблонов, имеет «непривычный» вид. Например, для явной схемы Бима-Уорминга (схема 92 в общем списке) с шаблоном
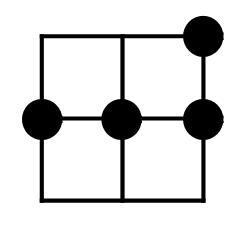 |
будет получено следующее выражение:
а для схемы с шаблоном (схема 29)
выражение:
Преобразуем подобные выражения так, чтобы они соответствовали виду уравнения переноса
Для этого заменим в полученных выражениях число Куранта \(r\) на соответствующее ему выражение \(r\to \frac{c\cdot {\rm\tau }}{h}\), но не везде, а только в числителе и, кроме того, квадрат от \(r\)(если он присутствует в числителе) заменим следующим образом:
После этого, в выражениях появится константа \(c\), но только в первой степени. Группировка коэффициентов при константе \(c\) приводит выражение (3.13) к виду:
Из формулы (3.14) аналогичным образом получаем:
Описанная процедура в большинстве случаев позволяет получить приемлемый вид разностной схемы. При необходимости, дальнейшие преобразования не сложно проделать вручную. Код, реализующий описанный алгоритм, приведен ниже:
| BuildShOut[sch_]:= Module[{num, den, cc, cct, ccx, shout}, num= Numerator@Together[sch]*h; den = Denominator@Together[sch]*h; num = Simplify[num /. {r^n_ -> p[n]*c*τ/h, r -> c*τ/h}]; num = num /. p[n_] -> r^n; cc = CoefficientList[num, c]; cct = Simplify[cc/den*τ]; cct = Collect[Numerator@cct, u[_, _], Factor] / Collect[Denominator@cct, τ, Factor]; ccx = Simplify[cc/den*h]; ccx = Collect[Numerator@ccx, u[_, _], Factor] / Collect[Denominator@ccx, h, Factor]; shout = {cct, ccx} /. u[i_, n_] -> SubsuperscriptBox[φ, i, n]; Return[shout]; ]; |
|
| sсhout = BuildShOut[sсh]; | (* символьное представление схемы *) |
numt = Numerator@shout; numx = Numerator@shout; dent = Denominator@shout; denx = Denominator@shout; (* формируем выражение для выдачи в файл: *) out=Style[ TraditionalForm @ DisplayForm@ RowBox[ {FractionBox[numt // TraditionalForm, If[dent === 1, \(\tau\), (dent*\(\tau\)) // TraditionalForm]], "+", c, FractionBox[numx // TraditionalForm, If[den2 === 1, h, (denx*h) // TraditionalForm]], "=", 0}], FontSize -> 24, Bold]; |
|