Проанализируем диссипативные и дисперсионные свойства схемы Лакса-Вендроффа. Как и схема «уголок» она является явной и двухслойной, однако в отличие от первой имеет второй порядок аппроксимации. Подставляя частное решение (2.38) в (2.28), приходим к характеристическому уравнению:
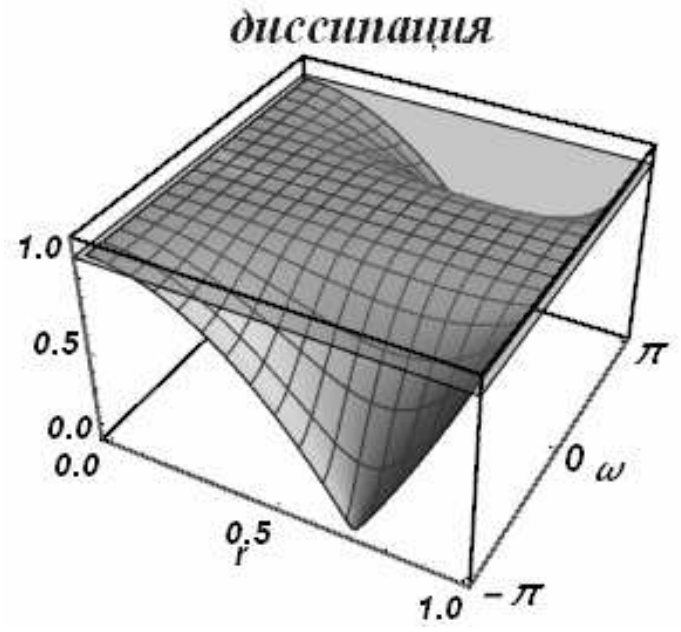
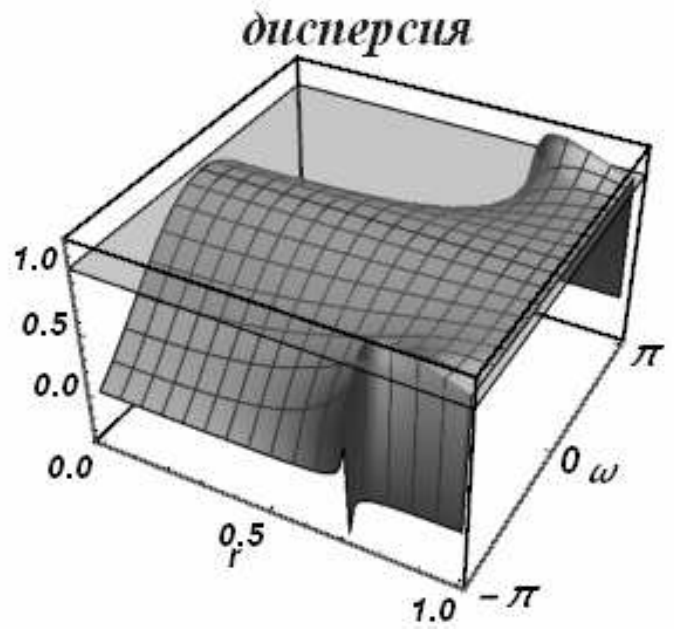
Можно показать, что модуль перехода будет меньше или равен единице при числах Куранта от нуля до единицы. На рис. 10 приведены диссипативная (слева) и дисперсионная (справа) поверхности схемы Лакса-Вендроффа. Если сравнить их с соответствующими поверхностями схемы «уголок», то видно, что качественно они похожи. Диссипативная поверхность схемы Лакса-Вендроффа при малых \(kh\)плотнее прилегает к единичной плоскости, что говорит о ее более высоком порядке аппроксимации и меньшей диссипативности. О дисперсионной поверхности можно сказать то же самое.
 |
 |
| а) | б) |
| Рис. 10. Диссипативная и дисперсионная поверхности схемы Лакса-Вендроффа | |
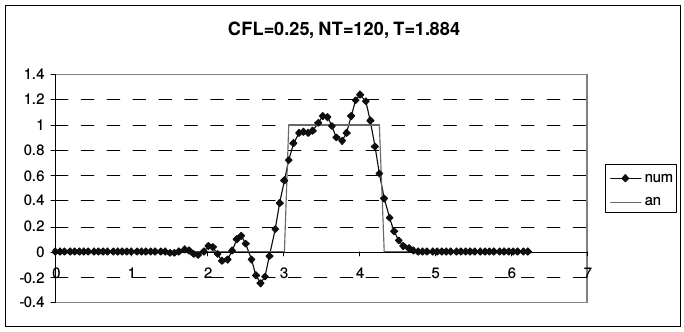
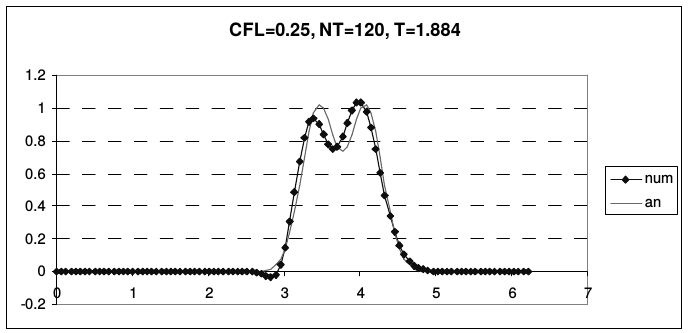
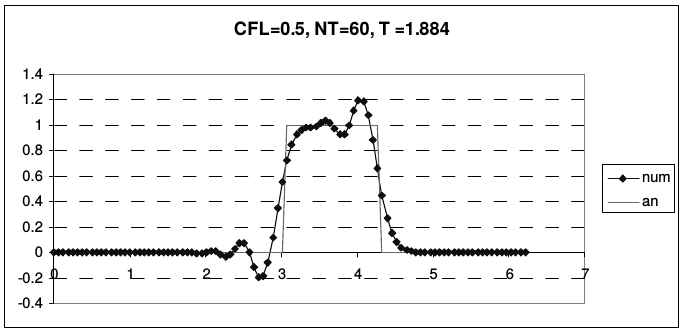
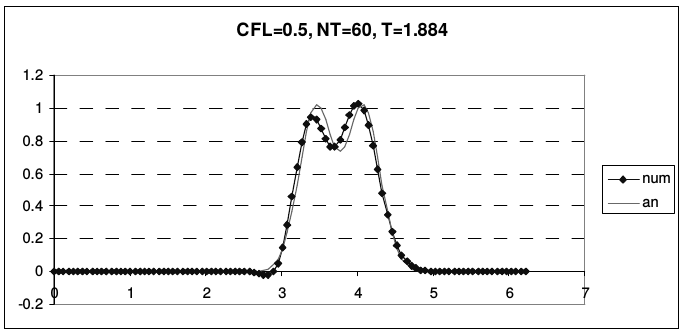
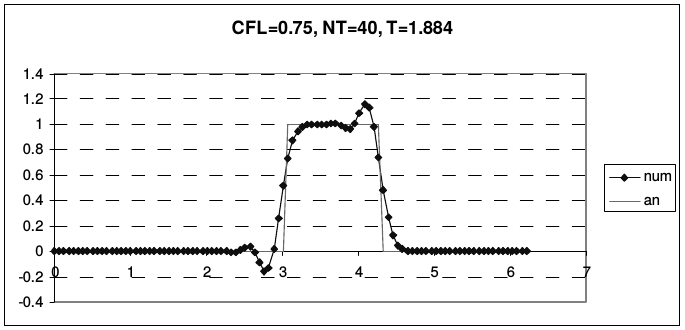
Рис. 11 иллюстрирует транспортные свойства схемы Лакса-Вендроффа на описанной ранее задаче о переносе начальных данных (2.43).
 |
 |
 |
 |
 |
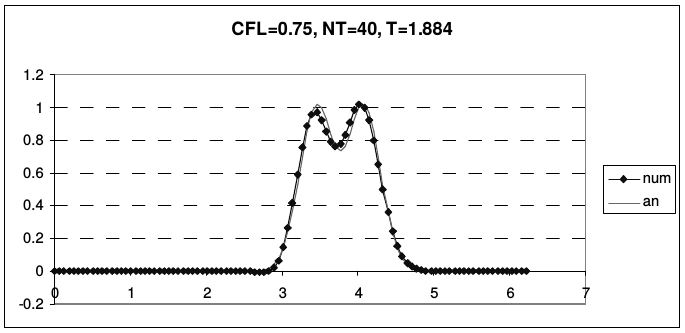 |
| Рис. 11. Результаты расчетов по схеме Лакса-Вендрофа | |