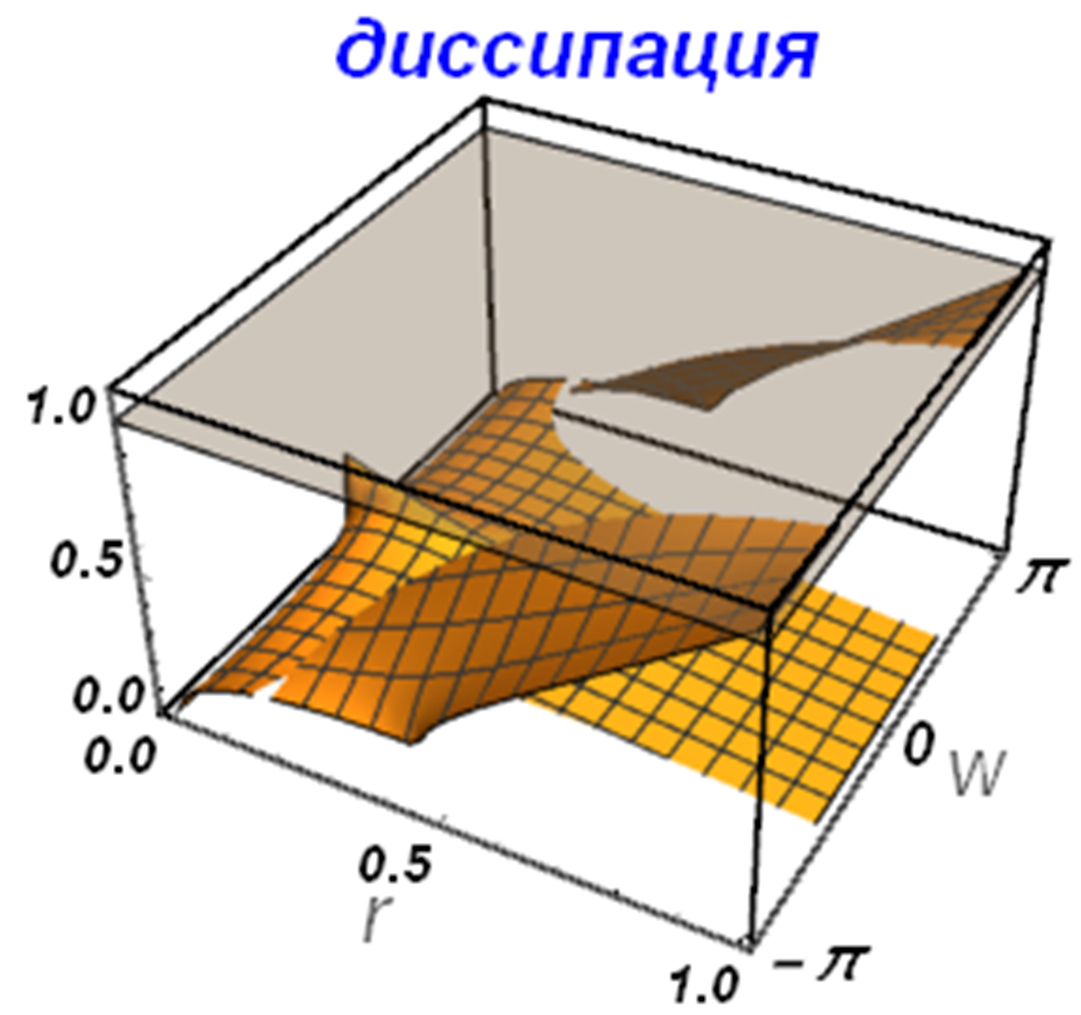
В заданном интервале устойчивости \(r_{\min } \le r\le r_{\max }\), \({\rm\omega }_{\min } \le {\rm\omega }\le {\rm\omega }_{\max }\) определим прямоугольную равномерную сетку точек, в которой найдем комплексные значения корней характеристического полинома. Для линейных полиномов, имеющих единственный корень, дополнительной обработки не требуется. Для квадратичных полиномов требуется провести сортировку корней. Причина, по которой необходима сортировка, следующая. Стандартная функция Sqrt[] системы Mathematica ведет себя так, что для двух близких комплексных чисел \(q_1\) и \(q_2\), чаще всего, также близкими являются комплексные значения \(Sqrt[q_{1} ]\) и \(Sqrt[q_{2} ]\) (естественно, также будут близки значения \(-Sqrt[q_{1} ]\) и \(-Sqrt[q_{2} ]\)). Но, в некоторых случаях, корни меняются местами, и вместо этого близкими начинают считаться значения \(Sqrt[q_{1} ]\) и \(-Sqrt[q_{2} ]\) (вторая пара \(-Sqrt[q_{1} ]\) и \(Sqrt[q_{2} ]\)также близка). На рисунке 31 приведены диссипативные и дисперсионные поверхности, построенные по неотсортированным корням для схемы-10.
 |
|
| Рис. 31. | |
Можно заметить, что на этом рисунке представлены две гладкие поверхности, элементы которых переставлены. Таким образом, необходимо осуществить сортировку корней в каждой точке, чтобы каждый из корней давал гладкую поверхность.
Учитывая, что при \(w=-{\rm\pi }\) и \(w={\rm\pi }\) для одного и того же r коэффициенты полинома (а значит и значения корней) совпадают, сортировка производится от \(w=-{\rm\pi }\) до w = 0 и от \(w={\rm\pi }\) до \(w = 0\)следующим образом:
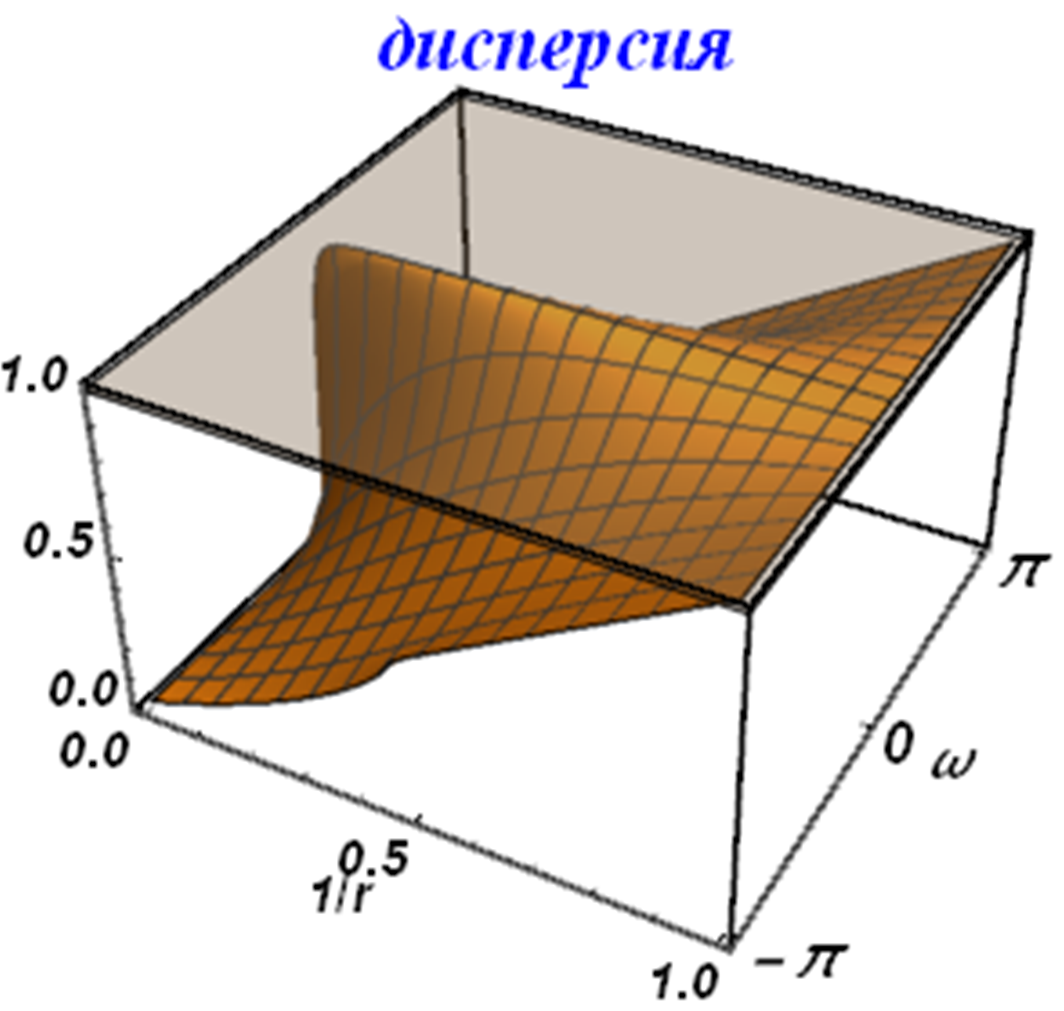
Результат работы этого алгоритма представлен на следующих рисунках:
 |
|
| Рис. 32. | |